|
Wind speed extrapolation
In wind energy studies, two mathematical models have
generally been used to model the vertical profile of wind speed over
regions of homogenous, flat terrain. The first approach, the log law,
has its origins in boundary layer flow in fluid mechanics and in
atmospheric research. It is based on a combination of theoretical and
empirical research. The second approach is the power law. Both
approaches are subject to uncertainty caused by the variable, complex
nature of turbulent flows.
(Manwell et al., Wind Energy Explained, Wiley, 2010)
Power Law
This calculator extrapolates the wind speed to a certain height by using the power law,
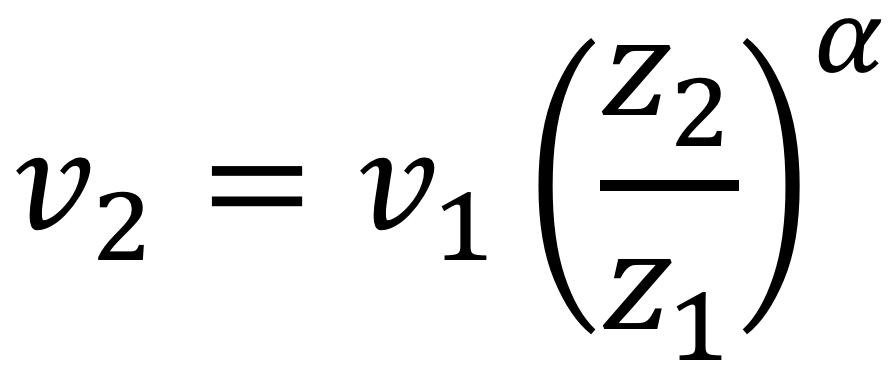
where:
- v1 = velocity at height z1
- v2 = velocity at height z2
- z1 = height 1 (lower)
- z2 = height 2 (upper)
- α = wind shear exponent
Wind
shear is quantified as the exponent α in the power law equation
that relates wind speeds at two different heights. It is important to
perform shear calculations only where valid upper and lower wind speed
measurements were available for a given time interval. In practice, it
has been found that α varies with such parameters as elevation, time of
day, season, temperature, terrain, and atmospheric stability. The
larger the exponent the larger the vertical gradient in the wind speed.
Although the power law is a useful engineering approximation of the
average wind speed profile, actual profiles will deviate from this
relationship.
To
determine the shear exponent between wind speeds at two heights, enter
values in the first four text boxes below. Then click the calculate
button, and the exponent value will appear in text box that equals α.
This calculator requires a JavaScript-enabled browser and the use
metric values. Metric conversion calculators can be found below.

|

|
|
|
Example:
v1 = 5.36 m/s (meters/second)
v2 = 5.72 m/s
z1 = 20 m
z2 = 30 m
α = 0.16
|
Extrapolate wind speed
To extraploate wind speed to a greater height, enter the
appropriate values in the first four text boxes. The calculated speed at height z3 will appear below. |
|
Example:
v1 = 5.54 m/s
z1 = 20 m
z3 = 80 m
α = 0.245
|
Log law
This calculator extrapolates the wind speed at a certain height by using the
log law. The increase of wind speed with height in the lowest 100m can
be described by the logarithmic expression
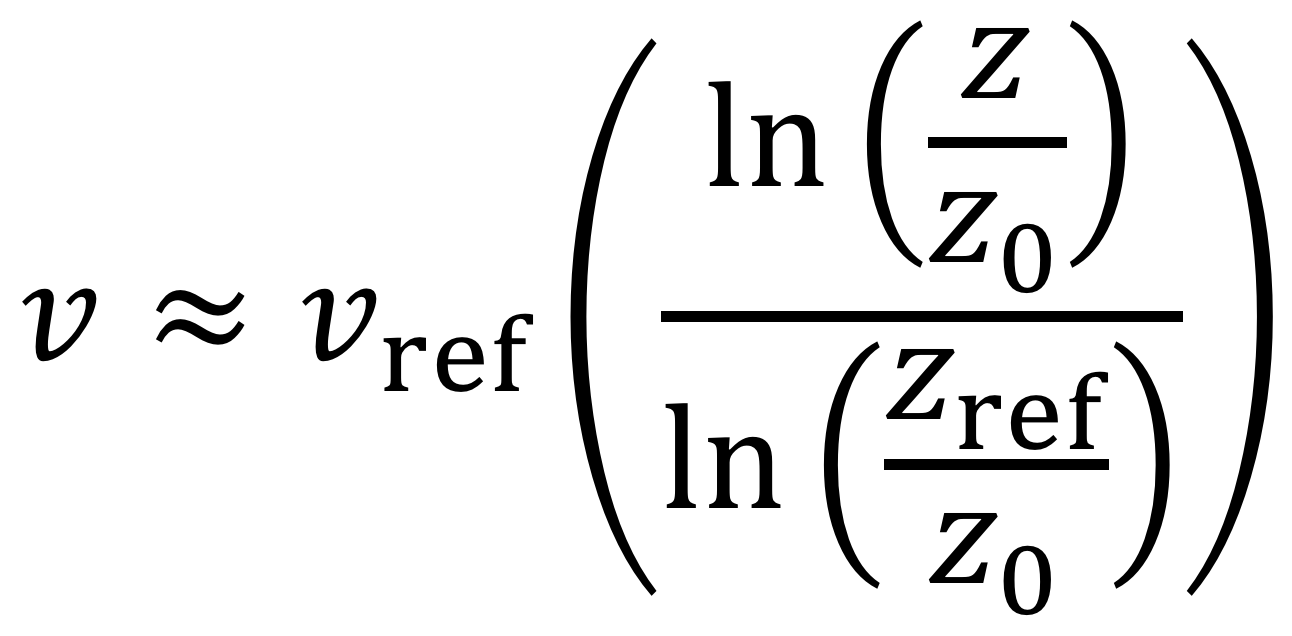
where:
- v = velocity to be calculated at height z
- z = height above ground level for velocity v
- vref = known velocity at height zref
- zref = reference height where vref is known
- z0 = roughness length in the current wind direction (see chart below)

|

|
|
|
Example:
vref = 6.6 m/s
zref = 30 m
z = 80 m
z0 = 0.4 m
v = 8.099 m/s
|
 |
 |
 |
| Roughness Class |
Roughness Length (m) |
Landscape Type |
 |
 |
 |
| 0 |
0.0002 |
Water surface |
 |
| 0.2 |
0.0005 |
Inlet water |
 |
| 0.5 |
0.0024 |
Completely open terrain with a smooth surface, e.g. concrete runways in airports, mowed grass, etc. |
 |
| 1 |
0.03 |
Open agricultural area without fences and hedgerows and very scattered buildings. Only softly rounded hills |
 |
| 1.5 |
0.055 |
Agricultural land with some houses and 8 metre tall sheltering hedgerows with a distance of approximately 1250 metres |
 |
| 2 |
0.1 |
Agricultural land with some houses and 8 metre tall sheltering hedgerows with a distance of approximately 500 metres |
 |
| 2.5 |
0.2 |
Agricultural
land with many houses, shrubs and plants, or 8 metre tall sheltering
hedgerows with a distance of approximately 250 metres |
 |
| 3 |
0.4 |
Villages, small towns, agricultural land with many or tall sheltering hedgerows, forests and very rough and uneven terrain |
 |
| 3.5 |
0.8 |
Larger cities with tall buildings |
 |
| 4 |
1.6 |
Very large cities with tall buildings and skyscrapers |
 Roughness definitions according to the European Wind Atlas. Roughness definitions according to the European Wind Atlas.
|
 |
|
|